Robotics
DH法
- a: z轴-z轴,沿x轴方向
- α:z轴-z轴的角度,z轴为旋转轴
- d:x轴-x轴,沿z轴方向
- θ:x轴-x轴的角度,z轴为旋转轴
homotopy continuation
- predict step+correction step
- bertini、julia homotopy、GPU-HC
Lie Group
- 扰动/导数用于优化,扰动模型导数更加简单
- 导数模型:
- 扰动模型:
Kinematics in Lie Group
- 即角速度与李群导数之间的关系
- 最简单的
就可以直接从数学上推导出来,但应该一种对应spatial velocity,另一种对应body velocity,物理意义是不同的 , ,
小波变换与傅里叶变换
- 傅里叶变换只能获取到频谱,但无法知道一开始是什么频率,后来是什么频率
- 傅里叶在突变点出会产生充斥整个时域的信号,小波只有在小波基对应的突变位置信号不为0,不会填充整个时域
- 小波变换存在尺度与平移量,用于控制小波基的深度与平移
LLM
attention
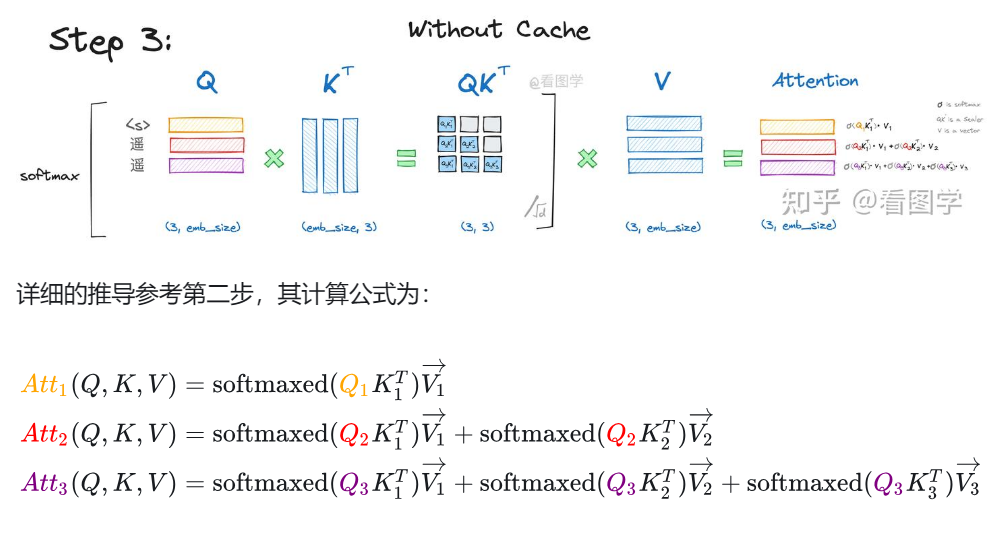
Q: 为什么要除以
A: 因为点积的数量级增长很大,很容易将softmax的一阶雅可比矩阵压缩到0附近,导致梯度消失。即有部分元素值很大,将softmax的输出压缩成一个由一个非常接近1和其余非常接近0的矩阵。
RoPE
旋转位置编码
对于最原始的正余弦编码而言,其预训练长度是固定的,如果训练了512个token,那么后续就只能处理512个token的输入,缺乏外推性。
因为attention的本质是内积,所以需要引入相对位置编码只需要在内积后保留相对位置即可。RoPE引入了复数作为旋转编码,给位置m的q乘以Rm,位置为n的k乘以Rn,得到的结果是q和k的内积乘以一个旋转矩阵。
infer加速技术
FlashAttention
- 通过降低存储访问开销来提升效率,虽然FLOPS会上升
- 通过分块的方式来对大矩阵乘法和softmax进行缓存
PagedAttention
- VLLM的关键加速组件
- 将虚拟内存的技术引入到LLM中
- 主要是对KV-Cache的进行分页优化
- 具有虚拟内存的优势,比如可以对cache快速进行内存共享
KV-Cache
- 针对decoder-only的自回归模型
- 因为causal mask的存在,被mask掉的部分不会参与到attention的计算,所以可以直接将前面的result缓存起来留作后用
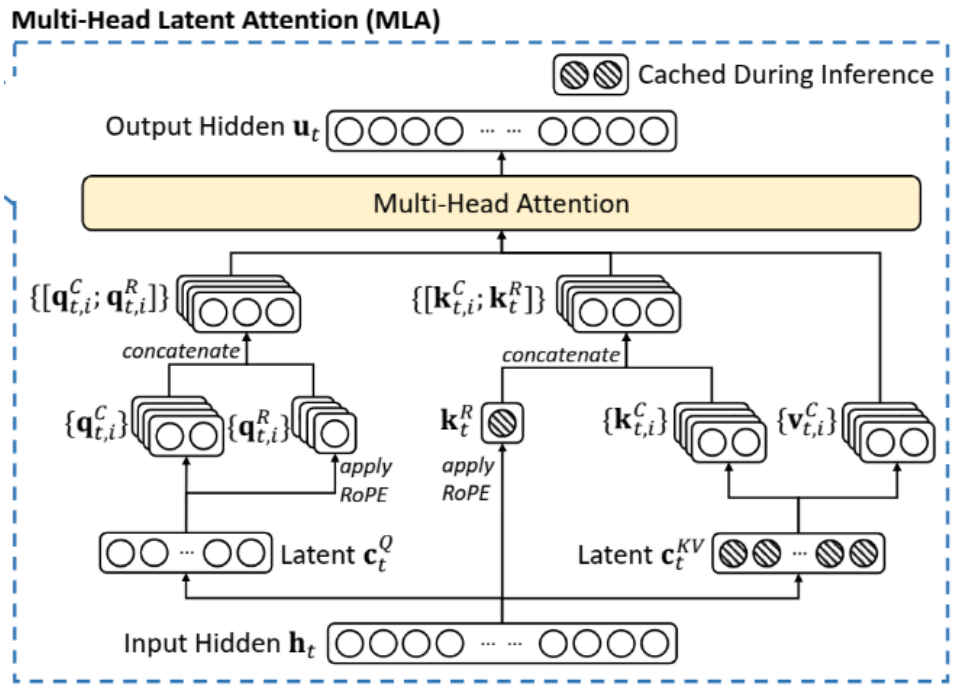
GQA MQA MLA
muti-head attention因为KV太多了,性能下降严重,所以产生了GQA MQA。其中MQA即muti query attention,GQA即grouped query attention。MQA中每个head共享K和V矩阵,kv cache直接下降到1/n。但MQA性能折扣严重,所以又产生了GQA,即将Q分成多个组,每个组对应一个K和V矩阵。一般的llm,比如LLAMA都是用的GQA。
而MLA即multi head latent attention,利用LORA的思想,将QKV分解成低秩的向量,然后公用矩阵缓存起来,私有矩阵直接被吸收掉了。另外为了处理RoPE,额外使用一部分维度来单独进行编码。
VLA
openvla
- dino v2 + siglip来对图像进行编码
- 图像编码后结果+指令编码后结果输入llama最后decode出action
DINO V2
- 自监督
- teacher+student,teacher不直接梯度更新,用指数平均移动从student获取权重
- 跟bert训练类似(bert预测遮罩词、预测两句连贯性),将部分patch只提供给teacher并让student与teacher输出接近;用student预测几个patch是来自同一图像还是不同图像
- 训练过程中尽量保持student与teacher的特征表示尽可能接近
SIGLIP与CLIP
- SIGLIP是CLIP的一个变种,用sigmoid loss取代CLIP中的softmax
- CLIP用vit来对图像进行编码,分别使用图像对文字的距离和文字对图像的距离来作为loss
Uniact
- 将原子行为编码为codebook,用token表示,从而实现跨平台
diffusion policy、DP3、iDP3
- diffusion policy即将DDPM扩展应用到VLA,输出从图像变为了action
- DP3即将点云作为diffusion policy的输入,能够以概率方式处理等价action,会使用MLP来编码点云
- iDP3即将DP3的world坐标系变为自身坐标系,同时在真机上应用
相机标定
射影空间
射影空间为齐次表示下引入,不存在平行线,欧式空间平行线相较于无穷远直线/平面,欧式空间中圆全部经过虚圆点/绝对二次曲线。标定相机就是在标定绝对二次曲线(IAC,或者说是“绝对二次曲线”在图像上的像),从而固定射影到欧式空间的度量。
标定相机就是在标定绝对二次曲线的像的推导
首先给出数学上的结论:绝对二次曲线的像(IAC,
- 而针孔成像模型:
,其中 为内参, 为外参。 - 对于空间无穷远点:齐次坐标写作
(方向向量 与最后一维 0)。投影到图像: ;平移 被消去,只剩 。 - 绝对二次曲面条件(复数域)给出方向满足
(经过虚圆点)。 - 将
用图像坐标表示: 。这样代回得到 (因为 )。 - 因此满足
的图像圆锥曲线矩阵为 。
(向量就是点,对称矩阵就是二次曲线)
(IAC也是纯虚点构成的,图像上不可见)
射影->欧式:把一条无穷远直线挑出来,然后在直线上挑出被称为虚圆点的点。
(2D下)由于射影变换仅比相似变换多四个自由度,仅从失真程度考虑(或者说度量性质),只要确定无穷远直线
(3D下)由于射影变换比相似变换多了八个自由度,因此需要确定一个无穷远平面,才能消除射影失真;确定绝对二次曲线,就可以消除仿射失真。(另外仿射变换维持了无穷远平面不变;相似变换没有改变绝对二次曲线)。最后,3D的平移与旋转可以被螺旋分解成单一轴的进动和旋转。
相机模型
给定相机投影矩阵
而投影矩阵前三列表示空间坐标系的xyz轴的消影点(
射影重构定理:当相机没有标定时,可以重建出无数个空间点集合,并且他们之间仅仅相差一个射影变换(射影多义性)。这造成了基本矩阵和本质矩阵之间的差异:本质矩阵能分解出唯一的外参,而基本矩阵只能分解出一个射影重构意义下的外参。(另一个表述:标定相机会出来的物体仅差一个相似变换;而未标定相机回复出来的物体相差一个投影变换)。