SLAM--三维刚体运动的理解

针对三维空间刚体运动的描述和个人的理解

三维空间刚体运动

欧式变化

旋转矩阵

先考虑旋转变化中的旋转矩阵。若某个单位正交基旋转后变为。考虑向量，由于其本身没有随着基旋转而旋转（相当于在世界坐标系中坐标未发生变化），所以用不同的基地表示出来的向量不应该发生任何变化，也就是两者相等，因此

两边左乘，并就可以写成如下形式

对于，其矩阵是两组基底的内积组成，而两个向量的内积恰好描述了其之间的相似程度(模长的乘积再乘以余弦值)，因此旋转矩阵可以看成是一个基底每个分量对于另一个基底的成分构成(因为都是单位基底，矩阵各个分量是各个基向量夹角的余弦值)。

同时，也正是因为是单位基底，所以旋转矩阵是一个行列式为1的正交矩阵，他的逆矩阵描述了相反的旋转变化。

平移变换

另外，欧式变换还包括平移变化，若将上式加上平移向量，那么有

这里指的是把坐标系2的向量变换到坐标系1，而指的是坐标系1原点指向坐标系2原点的向量，在坐标系1中的坐标。

如果单独把上式中的看成是在一个世界坐标系中取值为的点，那么可以得到一个更加直观的下式，其中描述的是从坐标系1的原点到世界坐标系中的位置，而指的是将坐标系2的向量进行旋转逆变换到坐标系1中，这样只要观察向量的下标，就更能清楚的看出欧式变换的关系。

另外，指的是坐标系1原点指向坐标系2原点的向量，在坐标系1中的坐标，而他的相反数指的是坐标系2原点指向坐标系1原点的向量，在坐标系2中的坐标，两者并不是相反数的关系。

因为由2指向1的那个向量在世界坐标系下是固定的，而坐标系2可以自由旋转，所以其在坐标系2下的取值是会发生改变的。如图。

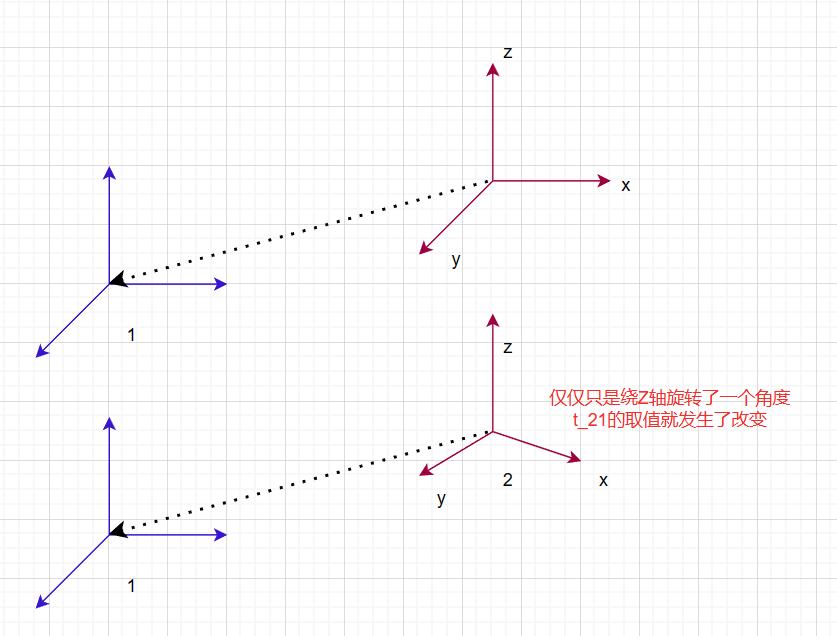
变换矩阵

对于

可以引入齐次坐标与变换矩阵，重写成以下形式

其中矩阵也被称为变换矩阵，这样能够更好的表示空间变换，它是一个4x4的矩阵。而额外增加一个维度的向量也被称为齐次坐标

旋转向量和欧拉角

旋转向量

旋转向量就是一个三维向量，它的方向为旋转轴，而模长为旋转角

旋转向量和旋转矩阵的关系如下

从第二个式子可以看出，旋转轴是旋转矩阵在特征值为1时对应的特征向量。

欧拉角

另一个描述旋转的东西为欧拉角，这个用的很多，也有著名的万向死锁问题，即第二次变换为±90°时，会导致第一次和第三次的旋转轴重合。

将三次变化依次记作 $、、$ ，由于欧拉角是存在先后作用顺序的，所以最终变换为

通过把每次变化的旋转矩阵写出来，令第二次变化的角度为90°，最后乘完了之后就能发现少一个维度，这个过程打起来不方便，就不再赘诉了。

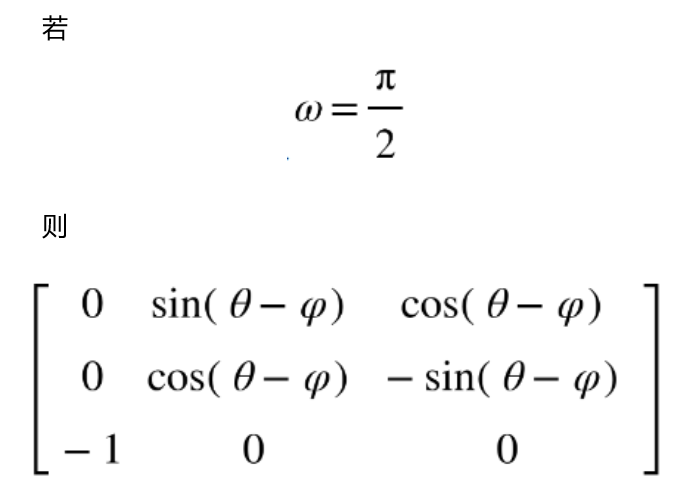
显然这时的值始终是-x了，不会发生改变。

四元数

旋转矩阵用9个量描述3自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但是带有奇异性。(所有三维向量描述都带有奇异性)

四元数来描述旋转既是紧凑的，又不带有奇异性。即

其中

它的加减乘除运算跟复数的运算相似。

四元数表示旋转

在二维平面，将一个向量乘上，可以看作是将这个向量旋转90°，所以我们可以用来描述二维平面的旋转，将表示旋转的向量与待旋转的向量相乘，得到的新向量就是旋转后的向量。

同理，用四元数表示旋转时，它有3个虚部和一个实部，虚部表示三维坐标系中的xyz，而实部是一个位于四维中的坐标平面，它和三维中每个坐标平面都垂直。

构造三维旋转的四元数向量为

而待旋转的向量为
那么旋转后的向量为

取出虚部对应的三个系数即为旋转后的坐标

个人的理解是这样的

考虑旋转为，且为了保证为单位四元数，取，即绕着z轴旋转

若三维向量

两者相乘，按照运算规则，显然

可以看出，此时x、y轴确实是发生了旋转90°(由[1,2]旋转为[-2,1])，但是z轴也被旋转到了四维空间的实轴上去了，如果是对一个空间物体施加这个旋转运动，那么旋转后的物体的z轴信息全部丢失了。也就是，仅仅左乘的旋转会导致真实物体一部分被映射到4维的超平面去，或者说，左乘四元数旋转向量会导致畸变。

既然左乘会引入畸变，导致一部分坐标被映射到四元数的实轴上去，那么自然会想到再成一个四元数向量来把抵消这个畸变。

如果仅仅是右乘一个同样的四元数，按照运算规则我们可以得到，可以看到右乘一个同样的四元数会施加一个反方向的旋转，且映射回来的z轴是反方向的。表现为物体在旋转轴方向呈现出堆成。

既然左乘是旋转，同时会把旋转轴正向映射到四维空间中；右乘是逆旋转，同时会把四维空间负向映射到旋转轴。那么只要右乘一个逆矩阵，不就是同向旋转，且同时把四维空间正向映射到旋转轴了嘛！

再次计算，此时的问题是旋转了两次90°，导致最终向量被旋转了180°。

所以既然左乘和右乘都会旋转一次，在最初构造旋转矩阵时就要把目标旋转角度除以2才行。即

总结一下规律

左乘四元数会正旋转，但是同时会把旋转轴正向映射到四维空间的实轴上，导致畸变
右乘四元数会逆旋转，同时会把四维空间的实轴反向映射到旋转轴上，左右同乘可以消除畸变
右乘四元数的逆会正旋转，同时会把四维空间的实轴正向映射到旋转轴上
所以通过左乘四元数和右乘四元数的逆，可以在不产生畸变的情况下旋转两次
所以在构造表示旋转的四元数时，需要把旋转角设置为1/2

四元数与其他表示形式的转换关系

若四元数表示为

定义

那么有

这样就可以分理至最后了

按照定义化简得到四元数到旋转矩阵的关系

由于旋转矩阵和旋转向量之间是存在迹的关系，所以两边取tr得到

结合之前的公式有

即

所以有四元数与旋转向量的关系

这个表达式正是之前我们用于构造出旋转的四元数，理论与实例得到了一致验证