SLAM-KF、位姿图、IMU优化

关于卡尔曼滤波器、以及位姿优化算法的学习

状态估计

之前我们可以从相邻的两帧图中获取到帧间的位姿，可以使用特征点法或光流法等，但是这种位姿可以看成是一种短期位姿，虽然我们在相邻两帧中使用大量点去尽可能减小估计误差，但是仍然存在全局的累进误差，或者说，使用这种方法估计出来的位姿是一种开环估计。但是此处我们不打算为其加入闭环部分，而是考虑长期位姿来对其进行补偿。

因为仅仅使用视觉里程计考虑两帧的位姿变化会存在累进误差，而我们对多个时间步得到的位姿进行滤波，这样就能进一步补偿视觉里程计计算出来的误差。

卡尔曼滤波器

卡尔曼滤波是一种带有马尔可夫假设的滤波方法，也就是当前时刻仅仅与上一时刻的状态有关，与更早的状态无关。

关于卡尔曼滤波器可以参考这篇文章，写的非常详细，我再添加一些自己的理解简略阐述一下。

卡尔曼滤波器其实就是将预测状态量的高斯分布和观测量的高斯分布融合为一个新的高斯分布，而新的高斯分布的均值和方差是原来两个高斯分布的一个加权，我们把这个加权记为卡尔曼增益，这个权重描述了我们到底是更相信我们的预测还是更相信我们的观测(因为无论预测还是观测都存在噪声)。

其中不确定性是使用协方差来描述，而更新协方差矩阵，也就是更新不确定性时，使用原有的不确定性和环境的不确定来共同完成

卡尔曼滤波的预测步：

其中，是状态量，是状态转移矩阵，是控制量，是协方差矩阵，是环境噪声的协方差矩阵。第一个式子描述使用上一时刻的观测估计混合值(也就是真值)和当前时刻的控制值来预测当前的状态，此时的是一个外部的控制量；第二个式子描述协方差矩阵的更新，是高斯分布下矩阵相乘后的协方差变化，而加法则描述了使用外部控制量时的不确定性。

卡尔曼滤波的的更新步：

其中，是卡尔曼增益，是观测矩阵，是观测噪声的协方差矩阵。第一个式子描述了卡尔曼增益的计算，卡尔曼增益描述了我们到底是更相信我们的预测还是更相信我们的观测；第二个式子描述了使用卡尔曼增益来更新状态量，是当前时刻的观测值，是当前时刻的预测值，描述了当前时刻的观测值与预测值的差距，而卡尔曼增益描述了我们对这个差距的信任程度，所以我们可以得到一个新的状态量；第三个式子描述了协方差矩阵的更新，描述了使用卡尔曼增益来更新协方差矩阵，也就是使用卡尔曼增益来更新不确定性。

为什么说卡尔曼增益就是两个高斯分布相乘时的权重呢

不加证明给出以下公式

对于

有

如果记

那么有

再看看卡尔曼滤波的更新步

考虑到高斯分布的第一个参数是均值，第二个参数是协方差，所以可以看到卡尔曼滤波中的K其实就是两个高斯分布乘积后再移去一个无关常数矩阵而已。而更新的和就是计算高斯分布乘积后更新后的均值与方差

至于为什么要把卡尔曼滤波的K矩阵省去一个常数矩阵，我认为是因为这个矩阵恰好是观测值与状态值的转移矩阵，而恰好是状态量乘以转移矩阵，而我们同时需要处理状态量与观测量，如果我们提前在K矩阵里把这个常数矩阵乘上，那么后续就需要计算该矩阵的逆，出于工程上的考虑，就把K矩阵中的这个常数矩阵省去了。或者说使用进行同维度的乘法(如果使用进行乘法需要计算逆矩阵)，最后在公式里能同时约去这个常数矩阵。

使用上述五个公式就可以构成卡尔曼滤波的计算，另外，由于卡尔曼滤波是求解的新高斯分布的均值，所以也是一种无偏估计。

图优化(BA)

从多个特征点发射出来的光线，会在几个相机的成像平面中汇聚到相机的光心，我们逐步对位姿和特征点位置进行优化，就能优化出理论的位姿和特征点的位置。

其损失函数就是观测的路标与相机模型计算出的路标投影的最小二乘，也就是重投影误差，而如果是多个位姿的优化，则可以把所有位姿对应的重投影误差加起来(但是第i时刻的位姿应该不会对其他时刻产生偏导，所以这也对应的增量矩阵的稀疏)。

我们之前已经计算过对于位姿的偏导和对特征点的偏导，理论上来说，可以直接利用各种优化算法来进行求解，但是，记为对相机位姿的偏导，为对特征点的偏导，那么显然我们使用高斯牛顿法进行增量迭代时，不难得出下式()

此时

当然，这个矩阵是稀疏的，因为每个路标只会影响到它观测到的特征点，所以我们可以使用Schur消元来简化这个矩阵。

其图优化和对应的矩阵如下所示

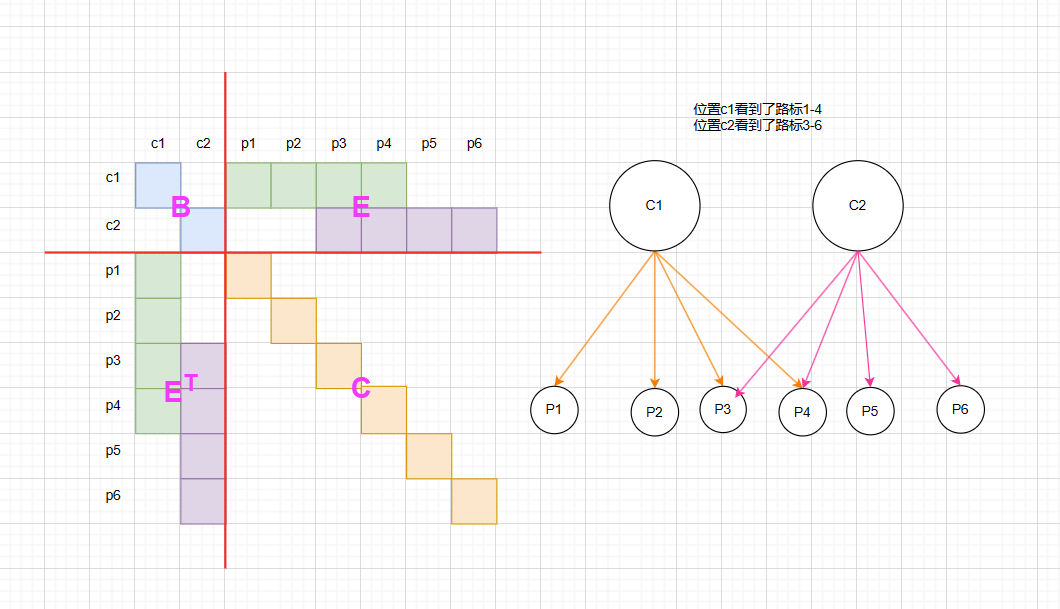
可以看到，因为特征点总数很多，所以这个矩阵维度会很大，但是我们观测的位置不一定很多，所以它会呈现出这样一种稀疏的结构，其中矩阵C是非常大的对角块矩阵，利用这个性质，我们在等式两边多乘一个东西，就得到了Schur消元的形式。

也就是

此时，第一行是一个与无关的东西，也就是边缘化了特征点，这样就不用去优化特征点了，只需要求解位姿即可。而且可以看到，矩阵C是一个对角块矩阵，每个块都很小，所以逆矩阵很好求，而剩余的仅仅只是矩阵的乘法，所以能大大降低运算量。

Schur消元物理意义

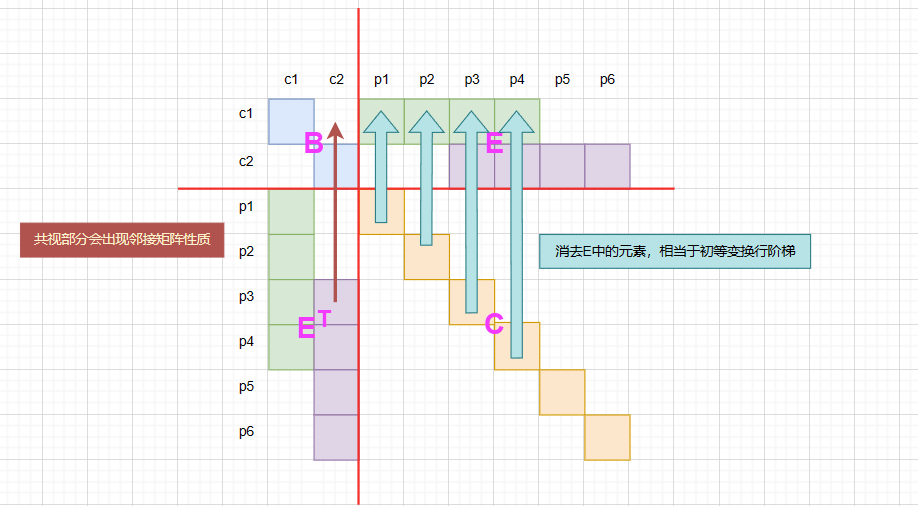
它的物理意义应该是使用初等变换去消去每一行中对于特征点的增量，也就是边缘化了特征点，这也很好理解为什么消元后有共视图的位置处会出现非0项

消元后的矩阵同样也描述了共视的信息，所以消元后的系数矩阵不一定是稀疏矩阵

滑动窗口

当然，上述BA是把每个时刻下的位姿和路径点都加入到优化中，这样时间一长，优化的规模就会不可控制。可以使用滑动窗口的方法，只保留最近的几个时刻的位姿和路径点，这样就能保证优化的规模。

滑动窗口主要有两个问题：

• 增加一个关键帧
• 删除一个关键帧

增加关键帧，只需要在之前的矩阵中增加一个位置和对应的关键点即可

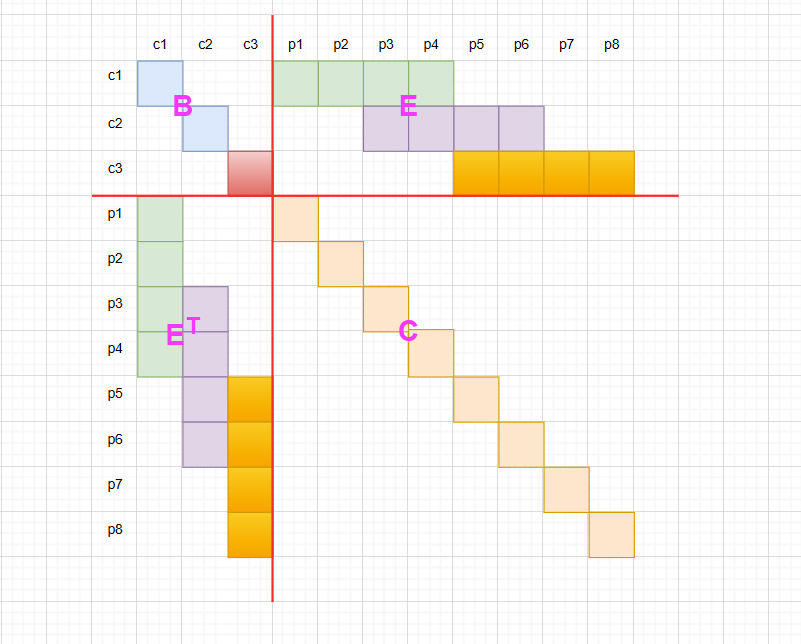
而删除关键帧就比较麻烦，因为需要边缘化位置c1，也就是需要使用类似初等变换的方法来让对应元素为0，这时就会导致矩阵不满足稀疏性质，导致计算量增大。

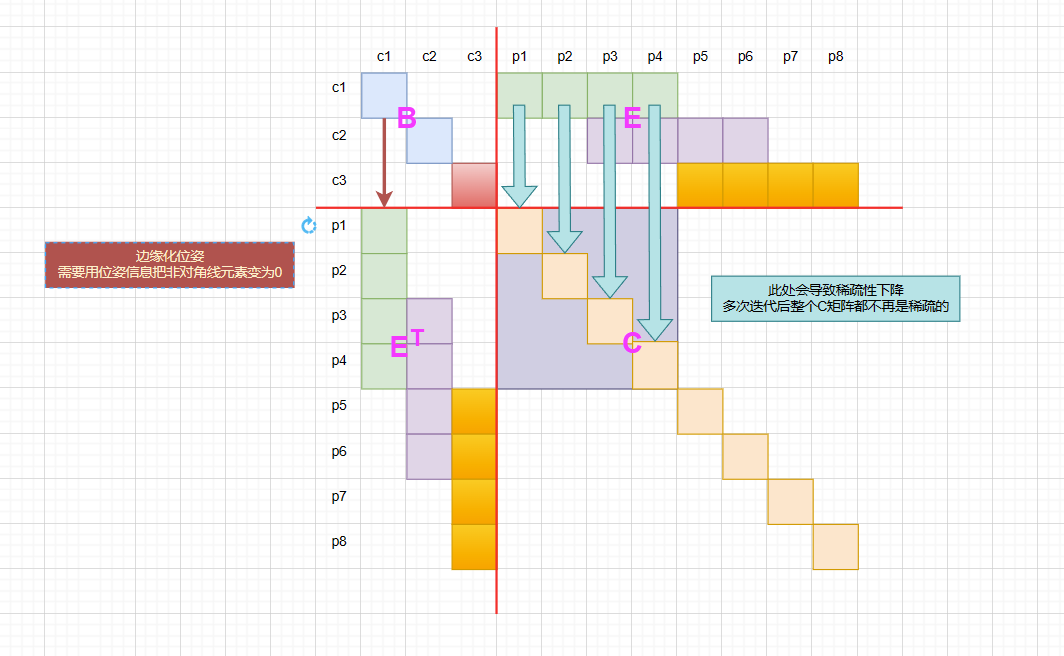
为什么不能直接删除？

因为根据图优化的原理，一个顶点与其他的顶点之间是存在连线(约束的)，如果要边缘化掉一个顶点，那么也就是消去其对应的约束，必然会转换成其他的信息，也就是位姿变换，直接删除掉并没有充分利用到这些信息。

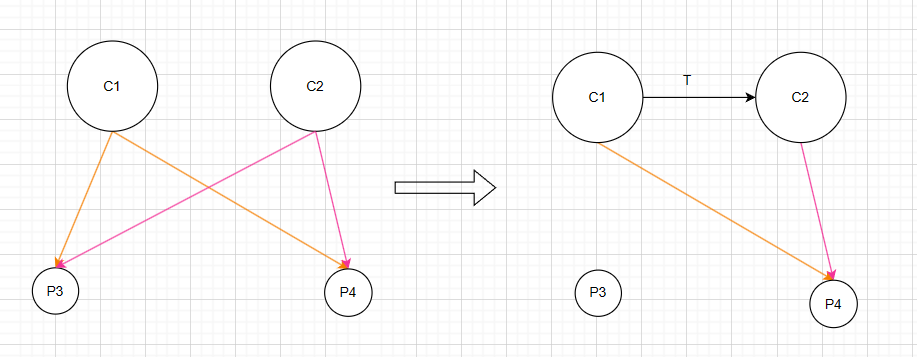
位姿图

在之前的优化中，我们最小化重投影误差，这要求同时优化特征点的空间位置和位姿，但是我们同样可以假设计算出来的特征点是正确的，仅仅去优化位姿，由于特征点数目很多，所以这样做能大大降低计算量。其图优化模型如下。

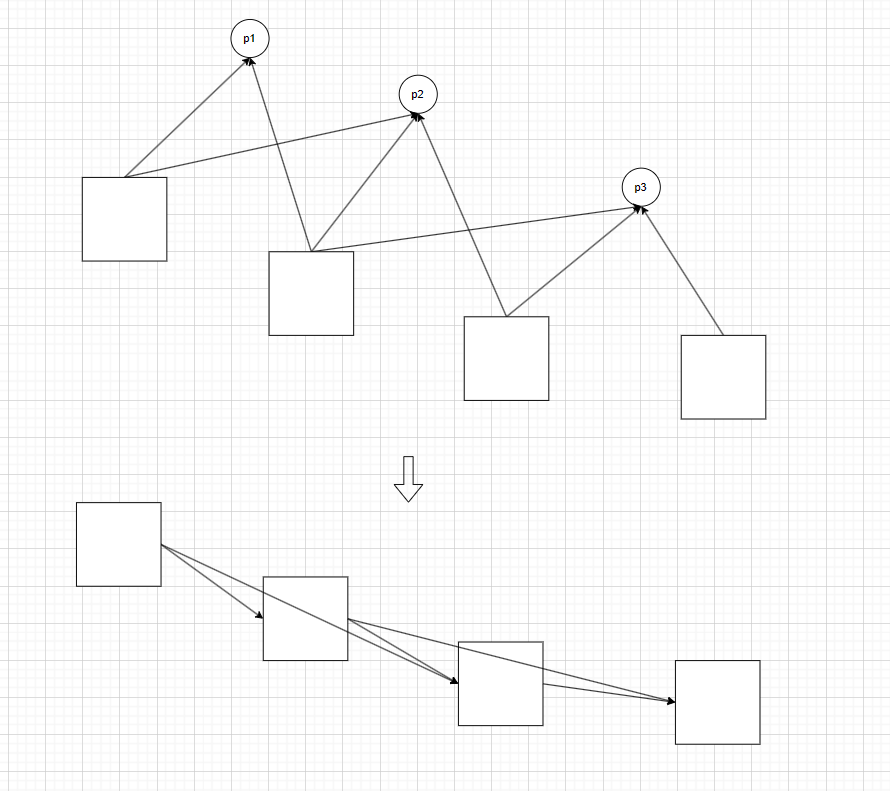
按照之前的理论，我们边缘化了所有的特征点，也就是把他们当作正确的东西来用，这时候，特征点与位置的边将全部消失，转换成各个位姿之间的联系。

所以，后续需要考量的就是如何把这些特征点与位姿的约束，转化成各个位姿之间的约束。此处太小写不下(公式太多了，不想写)