阅读g2o的综述论文,开始学习g2o
g2o: A General Framework for Graph Optimization
打算顺便学习一下图优化(g2o),所以先来看一下综述
g2o: A General Framework for Graph Optimization
图优化与SLAM
SLAM中许多非线性优化问题都可以转化成图优化,图的每个节点表示一个要优化的状态变量,而两个变量之间的每个边表示它连接的两个节点的约束信息(观察)。
当然,如果仅仅是针对非线性优化,目前已经有很多算法可以完成(比如牛顿法、高斯牛顿法等),但是如果转化成图优化,那么性能会更好
g2o框架提出来主要目的是:
- 提供一种简介的形式、统一的框架来供用户使用,通过少量代码来搭建图优化目标
- 提供优化性能很高的优化后端
而高性能主要是利用了
- 图的稀疏性
- 利用SLAM问题中图的特殊结构
- 求解稀疏线性系统的方法
- SMID等并行指令计算
由于在SLAM中,进行BA优化的时候需要使用到矩阵的稀疏性,所以在g2o出来之前,有PCG方法去求解稀疏的最小二乘、也有√SAM、iSAM这些高效的方法去求解稀疏最小二乘。而g2o也同样借鉴了这些算法的思想,并能提供一个统一的框架,并在所有的数据上都有较好的表现。
最小二乘的非线性图优化
在SLAM-KF、位姿图、IMU优化里,已经基本详细的介绍了稀疏矩阵的BA问题以及如何利用稀疏矩阵来求解,本综述中很大一部分内容也是在重述非线性稀疏最小二乘法如何利用稀疏矩阵来求解,所以这里就不再赘述了。
应用
在g2o中,只需要定义好误差项以及对应的加法(比如李代数的加运算),以及对应的雅可比矩阵的计算方式,就可以完成求解工作
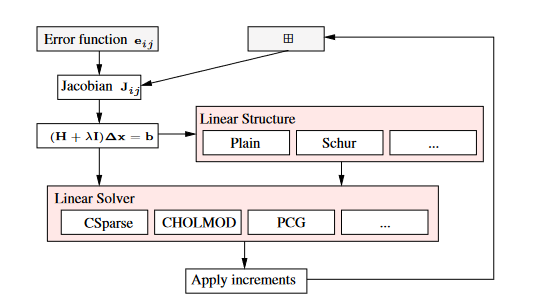
g2o通过为图中的顶点和边实现抽象基类来实现通用,这两个基类都提供了一组虚函数,以便于用户子类化,而大多数内部操作都是使用模板参数实现的,以提高效率。当然,为了快速性,也应用了SSE指令以及其他优化技术,例如惰性求值和循环展开等。
在g2o里还可以为问题指定特殊的结构,比如稀疏的schur消元;此外,还可以使用指定的求解器进行求解,比如选择PCG来求解稀疏结构。
g2o也与其他的方法进行了比较:如√SAM、SPA、sSBA、RobotVision。此外,这些方法仅仅针对一系列优化问题的子集,而g2o能够解决所有这些问题,并且还可以轻松扩展到新问题。可以看到g2o的速度基本上都是最高的那一档(虽然可能有时候算法都是一样的,但是g2o能用性能更高的前端生成优化问题)
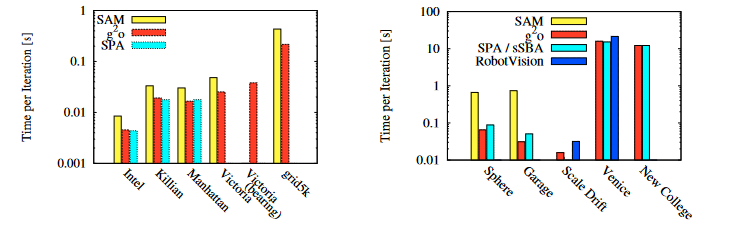
g2o可以使用简单的增加新的结点来扩展数据的数量;通过定义雅可比矩阵,可以简单的扩展新的问题。
可以看到,使用g2o可以快速定义问题,也可以高效的求解问题,而且图优化又可以很好的表示SLAM问题,所以g2o在SLAM中使用的非常多。