论文阅读--在RANSAC下基于HC和ML的位姿估计最小配置问题

阅读一下CVPR2022的Best Paper：Learning to Solve Hard Minimal Problems

Learning to Solve Hard Minimal Problems

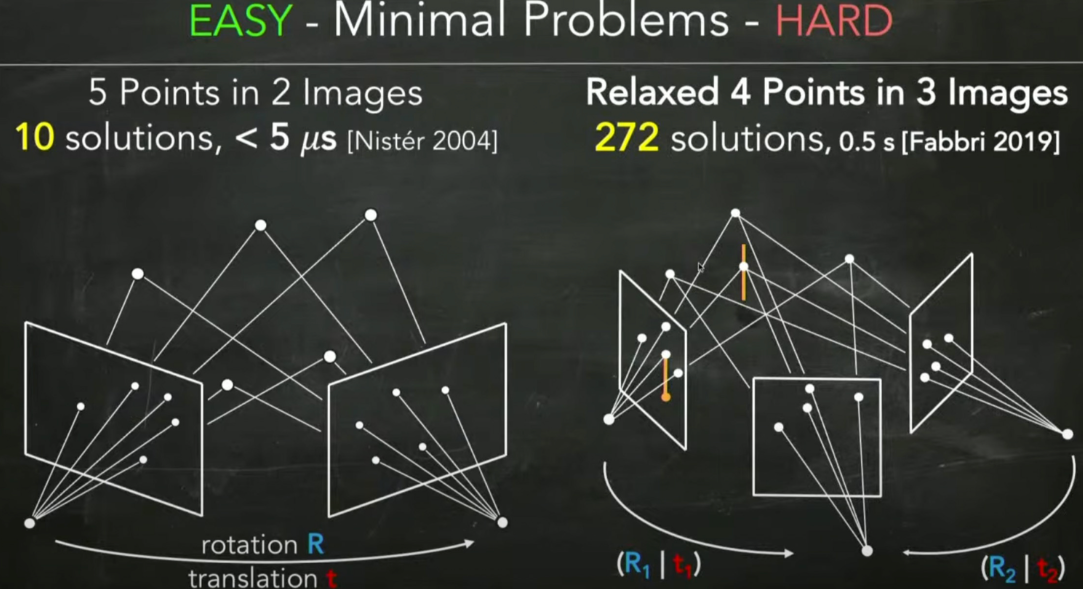
在2D-2D问题中，估计位姿求解本质矩阵的时候，如果仅仅考虑尺度放缩性，那么需要最少8点，而如果考虑旋转、平移的维度和尺度放缩性，那么最少只需要5点（这是针对两图估计一个位姿的情况，如果是三图估计两个位姿那么最少只需要4点）。这种用最少的维度来进行求解的问题就称为最小配置问题(Minimal Problems)。

由于在相机的位姿估计中，必须要保证所有的点在相机中的深度为正时才是有效的估计，而求解器在求解的时候往往会求解出一部分在相机中深度为负的解，这些解就称为伪解(spurious solutions)

由于伪解的存在，所以求解器在完成求解后还需要进行大量的验证工作来剔除伪解，而一旦问题的规模变大，那么验证的工作就会变得非常耗时，这篇文章就是提出了一种剔除伪解的方法，并显著加速。

同伦连续(HC)求解思路

由于本文的解法是基于HC的，所以先来看下HC的思想。

加入我需要求解的根，那么我可以构造一个函数，使得，而且的根是比较容易求解的，假如是"连续"的，那么就可以通过不断对进行增量来完成求解。

例如

其中是需要求解，但是求解起来很困难的，而是比较容易求解的，那么我们就可以通过不断增大来求解。但是显然，对进行递增时不一定保证对应的就是我们需要求解的，但是由于同伦的性质，每次对进行递增后得到的新的方程的解一定在递增前的解附近，这样我们选取上一次求解的作为初始值，并基于此来进行各种数值优化，从而就可以得到当前下的解。

在取不同值时对应的解连起来就能得到一条曲线，而就是需要求解的值，但是由于伪解的存在，且一条曲线只能对应一个解，所以显然需要有多个起点存在多条曲线来求解出所有的解，然后再进行剔除，这样一来HC方法的复杂度就上升了，因此求解效率也就变慢了。

算法概述

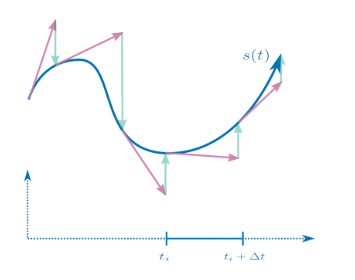
可以使用一个三次方程求根的例子来阐述一下算法的大概思路。

对于，下述方程而言，可以以为x轴和y轴，x的根为z轴，来绘制一个空间流形。

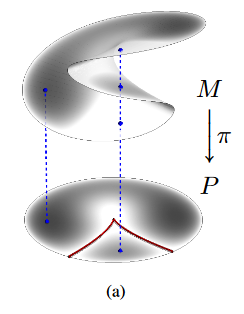
由于三次方程可能会出现三个根的情况(对应曲面重叠部分)，但对于这种存在多个根的情况，在位姿估计中往往只有一个根是有意义的，换句话说，某些根在问题集合中有意义的概率更大，因此我们可以通过学习的方式来找到这些有意义的根。在上图中，作者用灰色来表示"密度"，也就是哪些根是更有意义的。

而如果使用同伦连续(HC)的方法来进行求解，由于存在三个根，所以需要至少跟踪三条连续的曲线，并保证他最终收敛到不同的数值解上。然后接下来，并根据一定的规则去剔除的伪解。(因此，当问题的规模变大时，就需要跟踪很多曲线，这种方法的效率就会变得很低，这种方法称为先求解再剔除(solve-pick))

而如果，我们事先准备了大量的问题和对应的有意义的解(也就是problem-solution，或p-s pairs)，然后使用学习的方法学习出对于给定问题时，能够判断哪些起点构成的HC曲线以高概率收敛到真实的解上(也就是学习出上面的密度信息)，那么这样就只需要跟踪少量的曲线即可，这种方法称为先剔除再求解(pick-solve)。

第二种方法就是作者提出的新方法，下面就来进一步对这种方法进行阐述

算法结构

由于算法涉及到学习，所以肯定是先通过数据集训练好一个模型(offline stage)，然后再使用这个模型进行求解相关工作(online stage)。

训练(offline stage)：

根据数据和解的密度来构建能够较好描述目标场景的p-s集合，其中每个元素为一个problem-solution pair，也就是一个问题和对应的解
为数据集构造一个锚点的集合，每个锚点相当于一个起点，从这些起点出发的HC曲线能较好的覆盖数据集中的解空间
学习一个模型σ，用于判断给定的锚点是否能够收敛到当前问题的解上(此处相当于已经变成了分类问题)

求解(online stage)：

将问题表示成模型的输入形式(归一化等操作)
用学习好的模型挑选出锚点anchors
从锚点出发，求解出当前问题的解

我们还是先来看一下p-s集、anchor的构成，本文涉及到的模型非常简单(就是一个全连接神经网络)，所以关键还是在于如何表示问题。

构建p-s pair数据

我们的目标是使用5点来求解位姿，然后我们对某个场景采集了大量的数据D，下面我们需要根据这些采集的数据来构造数据集。

在文中，作者使用ETH 3D数据集，3D数据集中包含大量的3D点信息，所以可以直接在3D数据集中选择两个位置作为相机，然后选择这两个相机共视部分的5个特征点，接下来计算这5个3D特征点在两个相机上的投影坐标，一共5*2*2=20维，这样就得到了p-s pair中的p，也就是一个20维的向量；然后计算出这些3D特征点在两个图中的深度，可以得到2*5=10维，也就是p-s pair中的s，也就是一个10维的向量。

至此，我们就构建好了p-s pair。

Anchor

这篇论文的核心思想就在于通过神经网络来预测一个起始点，但可以想象，直接预测一个真实解附近的起始点是比较有难度的，所以作者就先从数据集生成多个起始点，称为anchor(锚点)，然后用神经网络来推断每个问题对应的anchor，这就类似于将回归问题转化成了分类问题。

那为什么可以通过选择anchor来作为起始点呢？假如，我们把一个个p-s看成是顶点，而从出发的HC曲线能通过优化够得到的解，那么我们就把两个点相连（并不意味着两者是同一个解，只是说明是他们的流形是十分接近的），这样就能构建出一个图。

而这个图理论上存在一个能够覆盖所有解的最小anchors集合，但是每个边求解是比较费力的，所以这种最小集合的求解是NP难的。作者在文中使用启发式算法来寻找一个较好的anchors集合

显然，当anchors集合越大，那么构建越耗时，但是能够较全面的覆盖所有解

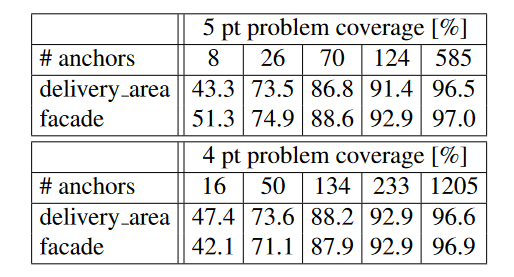
算法模型训练

上面描述了数据集的构建和锚点的选择，接下来就是模型的训练规则的问题了。

通过p-s生成数据集

我们之前不是已经得到p-s pairs了嘛？为什么还需要生成数据集？还记得我们之前说过模型做的是一个分类任务嘛，p-s pairs只有问题和对应的解，这一步做的工作是为每个problem打上关于anchor的标签。

模型输入数据就是p-s pair，如果是5pt问题，那么p是一个20维的向量，s是一个10维的向量。

那输出数据是什么？之前也说了模型本质是对多个anchors的分类的工作，这里的输出并不是anchors集合的one-hot格式的编码，而是anchors∪{TRASH}这样一个N+1个元素集合的one-hot编码，新增的这个TRASH label表示当前的anchors中不存在能够收敛到当前问题解的起始点，也就是说，如果模型输出的是TRASH，那么就说明当前问题在当前的anchors集合下无法求解出真实解。

训练任务

好了，现在输入输出数据都有了，下一步就是确定优化目标(损失函数)，这里的优化目标并不仅仅是问题求解的准确率，一方面是目前已经有一些算法能够耗时且准确的求解问题了，另一方面的话留到RANSAC部分具体阐述一下。优化目标是时间/准确率，即

当对模型输入一个p-s pair时，模型会首先对输入数据p进行归一化操作，然后输出一个|A|+1维的one-hot编码来表示哪个anchor最好，如果是TRASH的得分最高，那么就跳过当前数据，否则就跟踪得分最高的一条的anchor对应的HC曲线，然后进行优化，得到当前问题的解。(当然，输出层也是经过softmax后的，作者使用SGD优化器和交叉熵损失函数)

另外，由于可能存在多个anchor都能收敛到真实解，所以模型可能会返回多个anchor，后续的HC也会跟踪这些所有的anchors，然后可能会进行剔除操作，但是这与完整的HC相比，计算量和复杂度已经下降很多了。

为什么没有阐述一下模型

由于这个模型本质上就是一个分类模型，所以理论上所有分类模型的都可以用于此任务。

而原文中仅仅使用了一个8层全连接神经网络用于分类，所以这里就不再阐述了。

用于HC求解位姿的多项式

之前已经粗略的阐述过HC求解方法，下面以5pt求解位姿为例来阐述一下求解位姿的多项式结构。

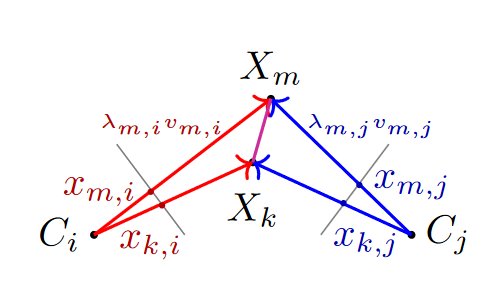
虽然位姿是改变的，但是任意两个特征点在3D空间的距离是不变的，因此可以利用特征的归一化坐标和深度来进行重投影。记为第个视图中的第个特征点的归一化坐标，为第个视图中的第个特征点的深度，那么可以得到

不过，由于位姿可以具有尺度不变性，所以可以令，这样就相当于是9个未知量(除去第一个点外的2*5-1个深度)和10个方程(组合数，任意两点都能有上述方程成立)

所以，对于5pt问题，可以使用本文的方法去求解上述方程即可，而且一定程度上可以避免剔除伪解的繁琐过程。

RANSAC

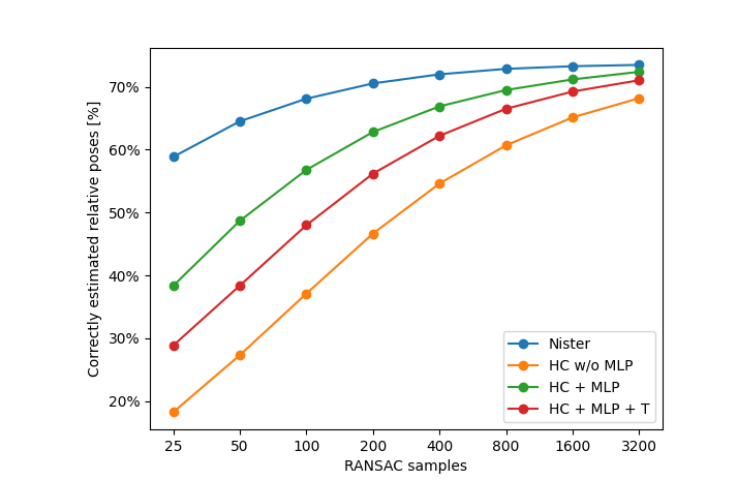
这里要首先阐述一下该算法与目前已有算法的对比实验结果。

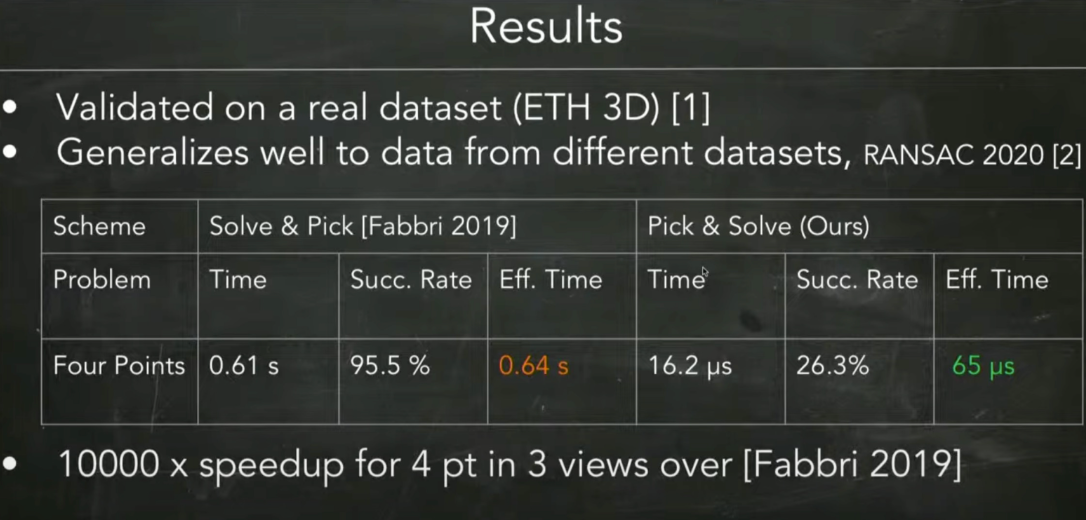
从上图可以看到，solve-pick算法的准确率是95.5%，耗时0.64s；而pick-solve算法的准确率是26.3%，耗时65us。

可以看到，本文的算法的速度快，但是准确率低，那么如何去综合描述速度-准确率之间的关系呢？换言之，如何去比较两个速度、准确率都不同的算法呢？

原文是这样说的，"目前的求解器的成功率接近100%，其误差仅来源于数据中的噪声和误匹配。因此，我们求解器在给定数据上的成功率为25%，所以我们期望它需要4倍于目前的求解器的样本数才能得到相同的结果"。

这说明，我们需要4倍数据才能得到近似目前的求解器的效果，因此我们要求此求解器比目前求解器快4倍才能有近似相同的速度。

至于为什么用4倍数据就能近似得到目前求解器的效果，这主要是使用了RANSAC框架。

RANSAC框架的思想很简单，就是不断从数据集中选出一个最小估计模型的子集作为数据集来估计模型。并把所有的数据带入这个模型，根据距离阈值计算内点(inner point)和外点(outer point)，内点是认为有效的数据；外点是认为是误差点。并最终返回能够让最多的点成为内点的模型。

举个例子

如果使用很多特征点来估计位姿，那么就按照下述步骤来执行：

从所有特征点中随机选择5个点（因为至少要5个点来估计本质矩阵）
用这5个点来估计本质矩阵，从而解出位姿
用求解的位姿分别计算左图的特征点在右图中的投影点，并与右图中实际点进行比较，如果距离小于阈值，那么就认为是内点，否则就是外点
统计内点的个数，如果内点个数大于之前的最大内点个数，那么就更新最大内点个数和对应的位姿
重复上述步骤，直到迭代结束或模型足够好（内点大于一定数目）

当然，实际上迭代次数是可以用极大似然估计来计算的，但是这里不做阐述。（因为是双变量，类似EM算法那种思路）

通过使用RANSAC框架，可以通过多次随机采样的方法来在一定程度上抵消掉本文中求解器的低精度，从而同时得到一个相对高速和高精度的求解器。