DLS、EPNP、UPNP算法学习与对比

阅读DLS、EPNP、UPNP三篇论文，对三种算法进行推导与对比。

PnP是通过n个点来估计位姿，比如P3P算法，如果n越多，那么就可以认为估计的位姿越来越准确，但是如果算法的复杂度随n的上升而快速上升，就会导致更多的点求解位姿时速度变得很慢，因此如果一个PnP算法的复杂度是O(n)的，那么理论上它就具有极高的精度和速度。所以我们这次来看一些具有O(n)复杂度的求解PnP的算法，先看下EPNP，然后是DLS和UPNP(Unified PnP)。

EPNP

论文地址

这篇论文的核心思想就是用4个控制点来表示出所有的点，这样无论估计多少个点，都会最终回归到使用4个控制点来估计位姿，而在计算控制点的复杂度是O(n)，这样就可以保证算法的复杂度是O(n)的。

控制点

假设空间下的点为，这里的上标表示空间坐标系，而记空间坐标系下的四个控制点分别为，其中。

理论上来说空间点是三维的，可以使用3个控制点就可以完全表示，但是为了更好的同时表示旋转和平移，空间都是使用齐次坐标，这样相当于就是4维的，所以需要4个控制点。

通过上式第二行可以看出，还应该有下式成立

只要上式中是可逆的，那么理论上可以随便选择一个可逆矩阵作为，那么就能满足约束。

对于如何计算出控制点，作者在文中特意提到了使用中心和特征值的方法。

我个人对这里的理解是：如果用控制点作为新的基底，然后使用归一化的坐标来原有空间点的齐次坐标进行表示，可以将原有的齐次坐标映射成另一个坐标，但是此时由于控制点任意，那么映射后的坐标是不定的，仅仅这样随意选取控制点去映射不能使得控制点综合所有空间点的信息，而如果实现给映射后的坐标值一个约束，即满足，那么相当于通过把所有空间点作为基底，而在一定约束下得到一个更高维度的控制点坐标，然后再反过来用新的映射后的控制点作为基底去重新表示所有的空间点，那么这样做的话，所有的控制点都相当于综合了所有空间点的信息。

上面是世界坐标系中空间点与控制点的关系，下面我们来看一下相机坐标系中的空间点与控制点的关系。

这里可以看到，由于这条性质的存在，相机坐标系和世界坐标系中的空间点与控制点的关系是一样的，也就是对应的是一样的，作者称其为homogeneous barycentric coordinates。

因此，我们只需要求解出控制点在相机坐标系下的坐标，就可以求解出所有空间点在相机坐标系下的坐标。

求解相机坐标系下的控制点

在求解之前，我们先来结合一下相机模型来看一下每个相机坐标系下的空间点的成像，并且把每个空间点用控制点来表示

显然，每一行都能得到一个方程，而利用第三行能消去，所以，这样每个点就能得到两个方程

由于需要求解的是相机坐标系下的控制点，也就是，所以我们可以把上面的两个方程写成矩阵的形式，可以得到下式

其中是4个相机坐标系下的控制点，也就是，而是一个的矩阵，其中是空间点的个数，也就是需要估计的点的个数。

上式可以看成是的零空间，也就是所有向量的空间的线性子空间，根据线代的理论，对应于零奇异值的A的右奇异向量形成了A的零空间的基，所以只需要求解出所有的右奇异向量，其线性排列就是所求解的目标值。

其中是右奇异向量。再考虑一下的右奇异向量的计算只需要计算，而是的矩阵，因此复杂度恒定为O(n)。

求解

上述解中除了右奇异向量外，还有一项非常重要的需要求解。而这里的并不一定恒定为4，原文中提到，如果相机焦距很小的时候，那么只有一个特征值会趋近于0，然而，随着焦距的增加，摄像机越来越接近正交，所有四个最小特征值都趋近于零。

考虑一下特征值与特征向量，如果特征值为0，那么，也就是说，的零空间的基就可以看成是的特征向量。而的特征向量恰好又是的右奇异向量。

因此，有几个特征值趋近于0，那么就说明解空间的基底个数有几个。

结合上面的分析，就可以知道总共会有N=1、2、3、4这四种情况，原文中对每一种情况都进行了讨论与计算，主要计算的方式就是两条原则

• 相机坐标系下控制点之间的距离 与 世界坐标系下控制点之间的距离是一样的
• 相机坐标系下的控制点是，而可以用和表示

通过上述方法就可以求解出的闭式解。

但是同样，如果把两个坐标系下控制点间距的差作为优化目标，也同样可以通过优化的方式求解，作者在原文中使用优化来对上述闭式解进行进一步的计算，从而得出一个更加精准的解，也就是优化下式。相当于使用上述闭式解来求解出一个非常好的初始值。

虽然这里其实是引入了迭代，但首先这其实是一个可选的步骤，之前的闭式解的精度也相当高了；其次，由于闭式解已经相当接近最优解了，所以迭代的次数不会很多，甚至可以设置成一个固定的迭代次数。因此不影响本算法的复杂度仍然为O(n)

在得到后，理论上就已经被求解出来了，接下来可以使用ICP去估计位姿了，此处就略过了。

ORB_SLAM2中的PnP求解器

ORB_SLAM2中的PnP求解器就是基于EPnP的，不过他在EPnP的外面包了一层RANSAC，它的核心代码基本跟上述步骤一致，此处先抛开RANSAC不谈，毕竟RANSAC的思想也不是很难。

但是ORB-SLAM2中一开始并不知道N的值，所以默认都是当作N=4来计算的，只不过由于N=4时未知量个数超过了方程个数，所以此处的做法是先提取出原方程的一部分来构成新的方程，使用SVD求解出这个方程后用优化的方法来进一步求解出，然后再求解出。

double PnPsolver::compute_pose(double R[3][3], double t[3])
    {
        // Step 1：获得EPnP算法中的四个控制点
        choose_control_points();

        // Step 2：计算世界坐标系下每个3D点用4个控制点线性表达时的系数alphas
        compute_barycentric_coordinates();

        // Step 3：构造M矩阵，EPnP原始论文中公式(3)(4)-->(5)(6)(7); 矩阵的大小为 2n*12 ,n 为使用的匹配点的对数
        CvMat *M = cvCreateMat(2 * number_of_correspondences, 12, CV_64F);

        // 根据每一对匹配点的数据来填充矩阵M中的数据
        // alphas:  世界坐标系下3D点用4个虚拟控制点表达时的系数
        // us:      图像坐标系下的2D点坐标
        for (int i = 0; i < number_of_correspondences; i++)
            fill_M(M, 2 * i, alphas + 4 * i, us[2 * i], us[2 * i + 1]);

        double mtm[12 * 12], d[12], ut[12 * 12];
        CvMat MtM = cvMat(12, 12, CV_64F, mtm);
        CvMat D = cvMat(12, 1, CV_64F, d);    // 这里实际是特征值
        CvMat Ut = cvMat(12, 12, CV_64F, ut); // 这里实际是特征向量

        // Step 4：求解Mx = 0

        // Step 4.1 先计算其中的特征向量vi
        // 求M'M
        cvMulTransposed(M, &MtM, 1);
        // 该函数实际是特征值分解，得到特征值D，特征向量ut，对应EPnP论文式(8)中的vi
        cvSVD(&MtM, &D, &Ut, 0, CV_SVD_MODIFY_A | CV_SVD_U_T);
        cvReleaseMat(&M);

        // Step 4.2 计算分情况讨论的时候需要用到的矩阵L和\rho
        // EPnP论文中式13中的L和\rho
        double l_6x10[6 * 10], rho[6];
        CvMat L_6x10 = cvMat(6, 10, CV_64F, l_6x10);
        CvMat Rho = cvMat(6, 1, CV_64F, rho);

        // 计算这两个量,6x10是先准备按照EPnP论文中的N=4来计算的
        compute_L_6x10(ut, l_6x10);
        compute_rho(rho);

        // Step 4.3 分情况去近似计算N=2,3,4时能够求解得到的相机位姿R,t并且得到平均重投影误差
        double Betas[4][4], // 本质上就四个beta1~4,但是这里有四种情况(第一维度表示)
            rep_errors[4];  // 重投影误差
        double Rs[4][3][3], // 每一种情况迭代优化后得到的旋转矩阵
            ts[4][3];       // 每一种情况迭代优化后得到的平移向量

        // 不管什么情况，都假设论文中N=4，并求解部分betas（如果全求解出来会有冲突）
        // 通过优化得到剩下的 betas
        // 最后计算R t

        // 求解近似解：N=4的情况
        find_betas_approx_1(&L_6x10, &Rho, Betas[1]);
        // 高斯牛顿法迭代优化得到 beta
        gauss_newton(&L_6x10, &Rho, Betas[1]);
        rep_errors[1] = compute_R_and_t(ut, Betas[1], Rs[1], ts[1]); // 注意是每对匹配点的平均的重投影误差

        // 求解近似解：N=2的情况
        find_betas_approx_2(&L_6x10, &Rho, Betas[2]);
        gauss_newton(&L_6x10, &Rho, Betas[2]);
        rep_errors[2] = compute_R_and_t(ut, Betas[2], Rs[2], ts[2]);

        // 求解近似解：N=3的情况
        find_betas_approx_3(&L_6x10, &Rho, Betas[3]);
        gauss_newton(&L_6x10, &Rho, Betas[3]);
        rep_errors[3] = compute_R_and_t(ut, Betas[3], Rs[3], ts[3]);

        // Step 5 看看哪种情况得到的效果最好,然后就选哪个
        int N = 1; 
        if (rep_errors[2] < rep_errors[1])
            N = 2;
        if (rep_errors[3] < rep_errors[N])
            N = 3;

        // Step 6 将最佳计算结果保存到返回计算结果用的变量中
        copy_R_and_t(Rs[N], ts[N], R, t);

        // Step 7 并且返回平均匹配点对的重投影误差,作为对相机位姿估计的评价
        return rep_errors[N];
    }

DLS

论文地址

DLS也是一种不错的PnP求解方法，下面也来阐述一下，不过这里的符号将不再和原文保持一致，因为后面一篇UPnP也存在类似的步骤。

问题建模

还是以最最常见的P3P来看一下，问题的建模非常简单，而我们的目标就是优化一个损失函数，让重投影误差最小。

上式中的是空间中的点，而是图像中的点，而是深度信息，这里的和是相机的旋转和平移，也是需要去求解的东西。那么就能得到下面的优化目标

理论上来说直接进行优化也不是不行，但是这会受到初始值得影响，不一定稳定；且运行速度上也可能会存在一定的问题。

DLS是这样处理的，下式中的移到左边去，然后再把所有的n写成矩阵的样子

也就是下式(这里应该都是矩阵/向量，只不过我最近生成latex公式的工具用的不太熟，改生成出来的latex源码实在是不方便，就懒得弄了)

然后我们求解，可以使用对求解伪逆来得到，也就是

注意这里的上面一直都是，而只有最后三个维度才是，所以我们可以利用分块矩阵来把拆开，得到下面的形式

这里相当于是求解出来的一种表示，我们可以借此把消掉，也就是把上式带回相机模型中，有

注意，之前是有n个以及、中各有3个自由度，一共是n+6个自由度，而现在的方程中已经把所有的和都消掉了，因此只有3个自由度。

接下来使用Cayley-Gibbs-Rodriguez (CGR) 参数化，目的是把分解成三个不相关的参数。

在说CGR参数化之前，先来说说为什么需要这么做。

首先，正常情况下需要表示一个旋转，往往只需要3个参数即可，而拥有9个参数，因此必然存在其他的约束，通常旋转矩阵具有下面两个约束

因为这两个约束的存在，会对直接求解旋转矩阵造成很多的麻烦，有时候人们会不管约束，直接求解旋转矩阵，再投影到一个最接近的欧式正交群的流形上来求解。而CGR就是把旋转矩阵分解成三个不相关的参数，这样就可以不用考虑约束的问题了。

CGR参数化只有简单的两个公式：

这里的，而表示反对称矩阵。

感觉网上也没有很具体阐述这个CGR参数化，好像大家都是直接拿来用的，也不知道是怎么推导出来的，好像只有在这篇文章有很少的一些解释

这种参数化最大的作用就是把旋转矩阵转化成无约束的形式，然后方便后续求解，可以看一下这里

在我们使用CGR参数化后，由于里面的主对角线上全部都是，因此他是一种线性的，所以可以直接把换成，这样就得到了

重写损失函数

因为通过CGR参数化，旋转矩阵已经不在具有约束，因此就可以转换成一种无约束的优化。

其中，也就是加上了一个噪声，然后将噪声单独分离出来

接下来的优化目标就是最小化这个噪声，这样相当于就能求解出旋转了，只要求解出旋转，那么就能回代到之前的式子中求解出平移

Macaulay matrix来直接求解

这部分可能理解存在偏差，如果有人知道这是怎么一回事欢迎交流下

文中又针对性的提出了一些更进一步的直接的解法，作者使用Bezout bound用于确定由损失函数的最优条件产生的多项式方程组的最大可能解数，通过使用Macaulay matrix来直接求解出所有的解。

这个Macaulay matrix也是一种求解多项式方程组的方法，不过有点难搞，跟后面的Grobner基一样，都不会具体阐述原理了。有一篇文章介绍了两者。另外，这个应该是用于研究此类的问题的库。

如果已经求出了最优解，那么每个偏导都将是等于0

但是关于的方程是一个四阶多项式系统，而上面仅有三个方程，如果不想去求解高阶线性方程组，那么就需要引入更多的约束来把每个高次项看成是新的变量来求解最小二乘解。如果想要增加更多的方程，就需要构造Maculy矩阵，首先作者对目标函数增加了i=0项，也就是

这里的都是随机生成的，然后通过把所有可能组成的七阶齐次项分配进四个集合，其中集合仅包含可以被整除的项，而集合包含所有剩余的项，也就是

然后用乘以中的每一个元素，就可以把每个扩展成，其中

然后通过在形式上的等效变换(即每个都是的各种多项式的线性组合)，就能得到Macaulay matrix ，这里的是集合的所有元素，而是剩余集合的所有元素。

由于（不包括，因为是随机构造出来的）是之前确认过为0的，而的形成仅仅是与其他什么东西相乘得到的，所以（i≠0）也是0，所以原方程就可以写成

这里把换成了，这个就是理论上的解，而之前的只是为了表示而已，要求解的东西也是。之前也说了无法把每个高阶项当作新的变量来求解，是因为方程数目不够，而这里扩充了方程的数目，理论上就可以来进行求解了(但是还是很奇怪有木有)

接下来通过矩阵分块可以得到一个特征值、特征向量的形式，因此只需要特征值分解就可以求出解了。

其中

当然DLS也可以用LM去优化之前那个式子，说实话，我感觉用优化或许更好理解一点...

UPNP

这个UPnP指的是Unified PnP，论文地址，从名字来看，这篇也是提出一个复杂度为O(n)的解法，可以在一定程度上看成是DLS的拓展，因为之前的EPnP和DLS都是针对光心位于相机坐标系原点的情况来考虑的，而这篇UPnP则考虑了光心不在相机坐标系原点下的更一般的情况的建模。

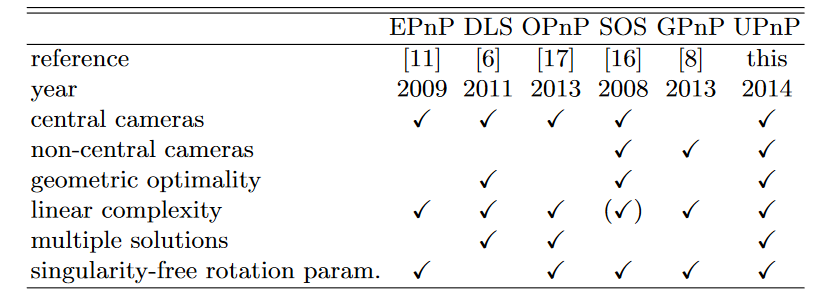
这个是作者关于各个算法之间的比较，可以看到列出的所有算法都是O(n)的，而仅有少数算法可以处理非中心光心的情况。此外，之前我们看到DLS是将旋转矩阵参数化成三个参数，因此会出现旋转奇点情况，而本文是参数化成了四元数，则不会有这种情况。

模型建立

下面是非中心光心下的模型示意图。

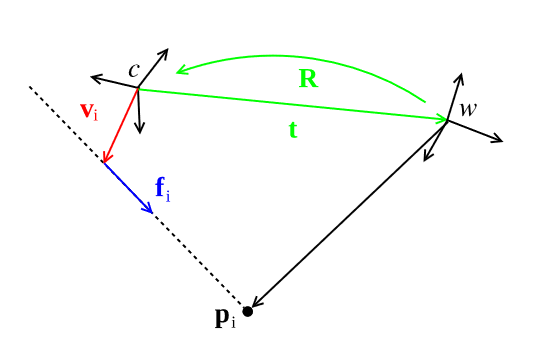
可以看到这种情况下出来的光线不会最终经过光心，因此这种情况下的模型会有所不一样。

相当于对之前的光心增加了偏移向量而已，然后接下来的处理也与DLS非常相似，也是先把移到左边去，然后构建成了矩阵形式

接下来也是非常熟悉的分块矩阵变换

要注意，这里面的矩阵是已知的，所以和也是可以求出来了，原文中也给出了求解后的结果，求解过程利用了舒尔补和，求解的结果以原文图片的形式直接放在下面了

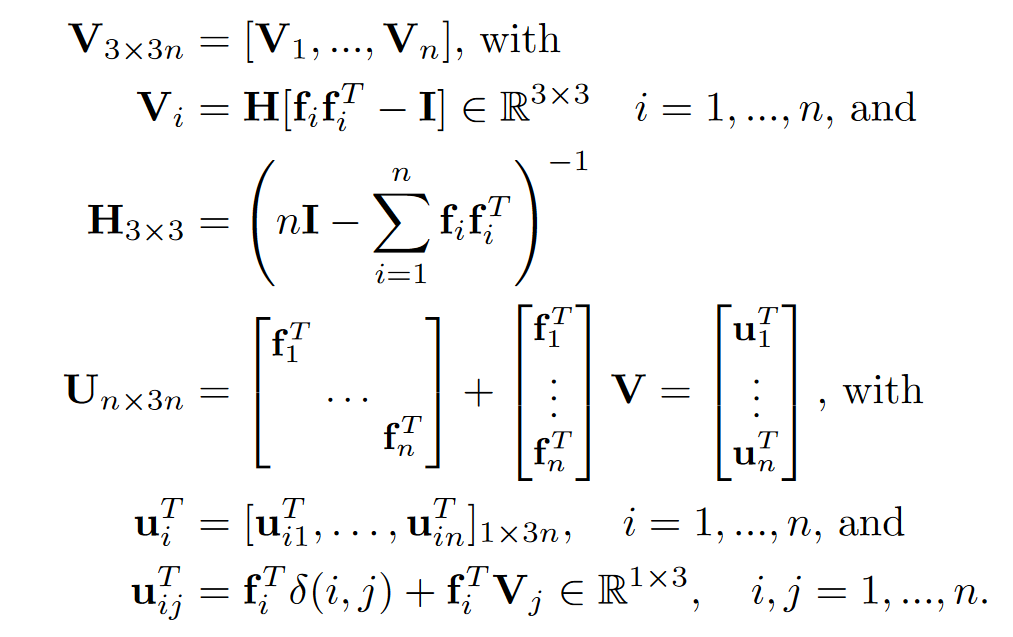
这里的是Kronecker symbol，当且仅当时，，否则，用来提取主对角线元素。

同样也能得到

同样可以导出优化目标，这里的类似于重投影误差

四元数参数化

然后使用四元数对旋转矩阵进行参数化(之前DLS使用CGR进行参数化，但是仅有3个维度会导致奇点问题)，这样做的目的是推导出一个O(n)复杂度的误差矩阵。

先放一个结论在这里，之前的可以表示成的形式，这里的是一个四元数中的二次项单项式组成的，而这里的、是可以直接计算出来的矩阵。下面来推导一下这个过程。

首先，先把之前的求出来，之前的是带有求和号的，这里把求和号展开求解，得到下式

其中，要看清楚这里的大V和小v哦，表示的是完全不同的东西，但是这两者之前已经描述过了，他们是可以直接计算出来的(因为是偏移，是分块矩阵的一个东西)，而上式中所有与不相关的东西都可以被直接计算出来，所以我们就把这一部分记作

接下来就需要对动手了，我们知道四元数和旋转矩阵可以一一转换，那么不妨假设我们的四元数是，那么对应的旋转矩阵为

其实这里就是把一个四元数转化成旋转矩阵，但是略有差别，因为这里是单位四元数，也就是，然后再把"1"代进去。看起来似乎有点复杂，但是每个元素都是二次项，这比CGR参数化后有更好的性质，如果我们把每个二次项排列出来定义出一个待求解的向量，也就是

考虑一下，对于点，那么经过四元数参数化后的变化后，的系数都是前面看到的四元数二次齐次项的形式，每个系数都是中的一个元素，所以如果我们把看作是一个系数向量，那反过来就能得到一个系数矩阵，也就是，其中如下所示，每个元素都是的元素

这样子，我们就可以把转化成，因此可以正式去对中的动手了，(动手的原因跟DLS一样，旋转矩阵带有额外的约束不好求，转化成无约束的形式求解才方便)

接下来再定义，因为这也是可以直接算出来的东西，那么我们就有了一个形式更加简洁的表达式

第二个等号这里我没看明白是怎么把提到前面去的，但是从维度的角度来说，变换前后确实没问题，不知道这里的理论依据是什么？

这里可以看到，我们最终把变成了一个的线性组合，而且这里的是一个四元数的二次齐次单项式组成的，而两个系数和都是可以直接利用之前的已知量计算出来的。

但我们最终需要的不是误差项，而是误差项的平方，而平方又可以写成转置与自身的相乘，因此有

这里的，利用了齐次坐标来转换成二次型

上面是对于单个点的误差，如果对所有点的误差进行求和就有

这个矩阵是由和组成的，所以它也是可以直接计算出来的，因此还是保证了O(n)的复杂度。

Gröbner basis求解方程组

上述可以使用优化法来进行求解旋转矩阵，但是与DLS一样，使用非迭代的方法来求解位姿的闭式解。之前DLS使用一个奇怪的Macaulay matrix来求解，而这里则是使用Gröbner basis来求解，明显UPnP的这个方法更加常见一点。

因为最优解一定是极值点，所以有导数等于0，这样就得到了4个方程

这里得到了四个方程，但是其实还有一个潜在的方程，因为这些方程都是二次齐次项，所以对于一个解来说，如果乘以一个常数，那么这个解也是成立的(简单看成和，那么,同时乘以一个常数还是原方程的解)，所以为了保证解有限个，再额外引入一个约束

这四个方程包含四个未知数，但是这是一个非线性方程，也就是四元二次方程组，之前DLS也遇到了这种高次方程组，而DLS是把所有的高次项看作是一个新的变量从而转化成线性方程并使用Macauly matrix来求解的。UPnP使用四元数参数化得到的高次方程组性质要好一点，因为每个高次项都是有且仅有二次，作者这里使用了Gröbner basis来求解。

关于Gröbner basis的具体内容，可以参考这篇和这篇，我个人对这里的理解也不是特别的充分，且原文这里说的感觉也是一笔略过的样子，就不班门弄斧了。

然后作者还探讨了一下使用带有单位矩阵约束的拉格朗日乘数法与Gröbner basis方法之间的差距，简单来说因为拉格朗日乘数法中要在极值点时为0，所以导致所以对于这样的约束其实是完全生效的，所以实际上拉格朗日求出来的解会更多(之前说过解乘以常数还是一个解)

二次对称性与二次最优

二次对称(2-fold symmetry)指的是q和-q对应的是同一个旋转矩阵，因为对旋转矩阵做四元数参数化时，所有的项要么是常数要么是二次项，负号全部对消。

而我们这里需要求解的多项式中虽然也都是平方或常数项，但是二次对称性会导致更多的解，这里的目的是在求解的过程中就直接避免这种情况的发生，因此在求解的过程中，我们需要引入一个额外的约束，这个约束是，然后对每个求导，就得到了奇次单项，这样就能保证解的唯一性了(因为平方或常数项才会导致对应同一个)。最终需要求解的就是这8个多项式：

openGV

openGV库实现了UPnP算法，当然还有一些其他的算法。编译这个库只需要安装Eigen3，我们要看的两个程序在test/test_absolute_pose.cpp和test/test_absolute_pose_sac.cpp中，前者是直接求解，后者是在RANSAC框架下进行求解。

不过这个库里的RANSAC没有UPnP的实现，需要自己稍微改一下程序添加进去看下效果。这里就简单跑2400个sample、用16个点估计位姿也就是P16P，看下准确率和平均时间

类型	无噪声无外点	2pixel噪声无外点	2pixel噪声10%外点	5pixel噪声10%外点	5pixel噪声20%外点
UPnP准确率	100%	100%	85.3%	82.4%	69.4%
UPnP每个sample耗时	0.68ms	0.69ms	0.68ms	0.69ms	0.68ms
UPnP-RANSAC准确率	100%	100%	100%	100%	100%
UPnP-RANSAC每个sample耗时	2.54ms	122ms	123ms	126ms	127ms

这里其实把生成数据的时间也统计进去了，如果只考虑UPnP本身的耗时的话，还会更低，这个算法效率真的挺高的。