Staskaer

Hi, this is Staskaer

0%

ORBSLAM2源码小记(3)--初始化器Initializer

Posted on Edited on In Valine:

ORBSLAM2的初始化器Initializer

主要是记录下相对容易忘的内容，不会写的很细

初始化器Initializer

初始化器仅用于单目SLAM，因为双目或RGBD本身已经有深度信息了，所以不需要初始化。此处略过一些通用性的基础内容，比如本质矩阵/单应矩阵求解，以及从其中恢复位姿的步骤。

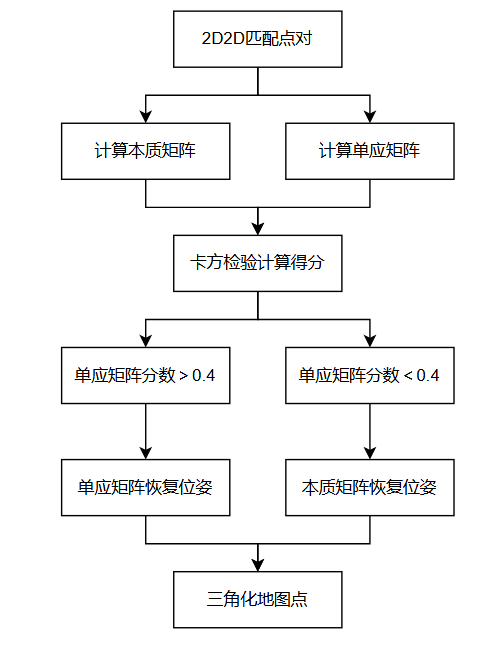
单目初始化器会同时计算本质矩阵和单应矩阵，在优先选择单应矩阵的基础上，选择得分更高的结果。

此处的得分是双向单应投影归一化坐标后的距离卡方拒绝域的距离。

卡方检验像素误差与分数计算

在计算本质/单应矩阵时，需要基于RANSAC来剔除外点，而剔除外点的原则时基于卡方检验。在计算前还会对特征点坐标进行归一化。

由于观测噪声默认是服从高斯分布的，而像素坐标系仅有两个自由度(u和v)，因此可以对单应/本质变换进行自由度为2的卡方检验，当单应/本质矩阵的双向投影误差过大时会认为对应的特征点在卡方检验的拒绝域内，这样就排除了外点。

2自由度卡方检验5%的显著性水平的拒绝域为5.99，其含义为"帧1中第i个匹配特征点投影到帧2后的投影误差"和"帧2中第i个匹配特征点投影到帧1后的投影误差"均小于5.99时，认为该匹配点是内点。

通过RANSAC算出来的得分最高的组的分数就是用于比较本质矩阵和单应矩阵的分数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
/**
* @brief 对给定的homography matrix打分,需要使用到卡方检验的知识
*
* @param[in] H21                       从参考帧到当前帧的单应矩阵
* @param[in] H12                       从当前帧到参考帧的单应矩阵
* @param[in] vbMatchesInliers          匹配好的特征点对的Inliers标记
* @param[in] sigma                     方差，默认为1
* @return float                        返回得分
*/
float Initializer::CheckHomography(
    const cv::Mat &H21,             // 从参考帧到当前帧的单应矩阵
    const cv::Mat &H12,             // 从当前帧到参考帧的单应矩阵
    vector<bool> &vbMatchesInliers, // 匹配好的特征点对的Inliers标记
    float sigma)                    // 估计误差
{
    // 说明：在已值n维观测数据误差服从N(0，sigma）的高斯分布时
    // 其误差加权最小二乘结果为  sum_error = SUM(e(i)^T * Q^(-1) * e(i))
    // 其中：e(i) = [e_x,e_y,...]^T, Q维观测数据协方差矩阵，即sigma * sigma组成的协方差矩阵
    // 误差加权最小二次结果越小，说明观测数据精度越高
    // 那么，score = SUM((th - e(i)^T * Q^(-1) * e(i)))的分数就越高
    // 算法目标： 检查单应变换矩阵
    // 检查方式：通过H矩阵，进行参考帧和当前帧之间的双向投影，并计算起加权最小二乘投影误差

    // 算法流程
    // input: 单应性矩阵 H21, H12, 匹配点集 mvKeys1
    //    do:
    //        for p1(i), p2(i) in mvKeys:
    //           error_i1 = ||p2(i) - H21 * p1(i)||2
    //           error_i2 = ||p1(i) - H12 * p2(i)||2
    //           
    //           # 这里的sigma默认为1
    //           w1 = 1 / sigma / sigma 
    //           w2 = 1 / sigma / sigma
    //
    //           if error1 < th
    //              score +=   th - error_i1 * w1
    //           if error2 < th
    //              score +=   th - error_i2 * w2
    //
    //           if error_1i > th or error_2i > th
    //              p1(i), p2(i) are inner points
    //              vbMatchesInliers(i) = true
    //           else
    //              p1(i), p2(i) are outliers
    //              vbMatchesInliers(i) = false
    //           end
    //        end
    //   output: score, inliers

    // 特点匹配个数
    const int N = mvMatches12.size();

    // 获取从参考帧到当前帧的单应矩阵的各个元素
    const float h{ij} = H21.at<float>(i, j);
    ...

    // 获取从当前帧到参考帧的单应矩阵的各个元素
    const float h{ij}inv = H12.at<float>(i, j);
    ...

    // 基于卡方检验计算出的阈值（假设测量有一个像素的偏差）
    // 自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值
    const float th = 5.991;

    // 加权系数，sigma为1，invSigmaSquare也为1
    const float invSigmaSquare = 1.0 / (sigma * sigma);

    // 通过H矩阵，进行参考帧和当前帧之间的双向投影，并计算起加权重投影误差
    // H21 表示从img1 到 img2的变换矩阵
    // H12 表示从img2 到 img1的变换矩阵
    for (int i = 0; i < N; i++)
    {
        bool bIn = true;

        // 提取参考帧和当前帧之间的特征匹配点对
        const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
        const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];
        const float u1 = kp1.pt.x;
        const float v1 = kp1.pt.y;
        const float u2 = kp2.pt.x;
        const float v2 = kp2.pt.y;

        // 计算 img2 到 img1 的重投影误差
        // x1 = H12*x2
        // 将图像2中的特征点通过单应变换投影到图像1中
        // |u1|   |h11inv h12inv h13inv||u2|   |u2in1|
        // |v1| = |h21inv h22inv h23inv||v2| = |v2in1| * w2in1inv
        // |1 |   |h31inv h32inv h33inv||1 |   |  1  |
        // 计算投影归一化坐标
        const float w2in1inv = 1.0 / (h31inv * u2 + h32inv * v2 + h33inv);
        const float u2in1 = (h11inv * u2 + h12inv * v2 + h13inv) * w2in1inv;
        const float v2in1 = (h21inv * u2 + h22inv * v2 + h23inv) * w2in1inv;

        // 计算投影误差 = ||p1(i) - H12 * p2(i)||^2 
        const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1);
        const float chiSquare1 = squareDist1 * invSigmaSquare;

        // 用阈值标记离群点，内点的话累加得分
        if (chiSquare1 > th)
            bIn = false;
        else
            // 误差越大，得分越低
            score += th - chiSquare1;

        // 计算从img1 到 img2 的投影变换误差
        // x1in2 = H21*x1
        // 将图像2中的特征点通过单应变换投影到图像1中
        // |u2|   |h11 h12 h13||u1|   |u1in2|
        // |v2| = |h21 h22 h23||v1| = |v1in2| * w1in2inv
        // |1 |   |h31 h32 h33||1 |   |  1  |
        // 计算投影归一化坐标
        const float w1in2inv = 1.0 / (h31 * u1 + h32 * v1 + h33);
        const float u1in2 = (h11 * u1 + h12 * v1 + h13) * w1in2inv;
        const float v1in2 = (h21 * u1 + h22 * v1 + h23) * w1in2inv;

        // 计算重投影误差
        const float squareDist2 = (u2 - u1in2) * (u2 - u1in2) + (v2 - v1in2) * (v2 - v1in2);
        const float chiSquare2 = squareDist2 * invSigmaSquare;

        // 用阈值标记离群点，内点的话累加得分
        if (chiSquare2 > th)
            bIn = false;
        else
            score += th - chiSquare2;

        // 如果从img2 到 img1 和 从img1 到img2的重投影误差均满足要求，则说明是Inlier point
        if (bIn)
            vbMatchesInliers[i] = true;
        else
            vbMatchesInliers[i] = false;
    }
    return score;
}

校验解

每个本质/单应矩阵可以分解出不止一对R和t，因此需要选出最好的R、t组合。至于本质/单应矩阵的分解和三角化求空间点比较基础就不再赘述了。

在分解出若干组R、t后，会选择使得相机前方产生最多3D点的R、t作为最终结果。